高二数学直线方程知识点总结（掌握直线方程）

直线方程是其中的重要内容之一，数学作为一门基础学科。能够灵活运用直线方程解题，在高二数学中，我们需要掌握直线方程的相关知识。帮助大家更好地理解和应用直线方程，本文将高二数学中的直线方程知识点。

一、直线的一般方程

B，C为实数且A和B不同时为0，直线的一般方程为Ax+By+C=0，其中A。这个方程可以表示平面上的任意一条直线。我们可以确定直线的斜率和截距，并且可以通过两点求出直线的一般方程，通过一般方程。

二、斜率截距式

其中k为直线的斜率，斜率截距式是直线方程的一种常用形式，b为直线与y轴的截距，表达为y=kx+b。并且可以方便地求出直线与坐标轴的交点、通过斜率截距式，我们可以根据直线的斜率和截距快速画出直线。

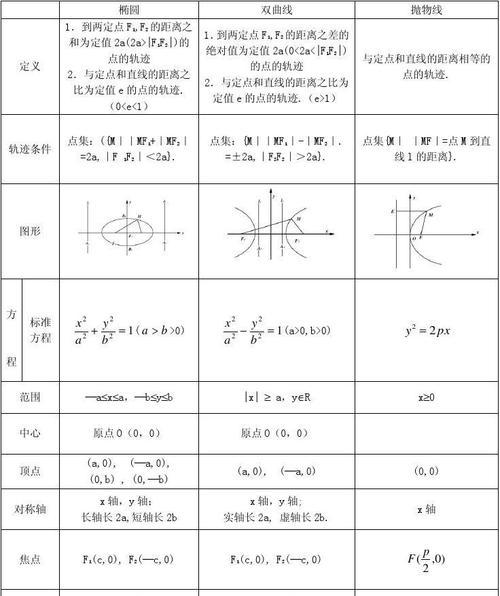
三、点斜式

表达为y、点斜式是直线方程的另一种形式-y?=k(x-k为直线的斜率，其中(x?,y?)为直线上的一点，x?)。我们可以根据直线上的一点和斜率确定直线方程、通过点斜式，也可以通过两点求出直线的点斜式。

四、两直线的关系

平行或重合，两条直线可以相交。我们可以确定两条直线的关系，通过判断两条直线的斜率和截距。它们具有相同的斜率但截距不相等，当两条直线平行时；它们具有相同的斜率和截距、当两条直线重合时。

五、平行线与垂直线的斜率关系

它们的斜率相等，当两条直线平行时；它们的斜率的乘积为、当两条直线互相垂直时-1。我们可以判断两条直线是否平行或垂直，并且可以求出与已知直线平行或垂直的直线方程、通过这一关系。

六、直线与圆的关系

直线与圆可以有三种关系：相切和相交，相离。我们可以确定直线与圆的关系，通过求解直线方程和圆的方程。直线与圆没有交点，相离时；直线与圆有且仅有一个交点，相切时；直线与圆有两个交点，相交时。

七、直线与函数的关系

直线与函数可以有三种关系：平行和重合，相交。我们可以确定直线与函数的关系、通过求解直线方程和函数的方程。直线与函数有一个交点、相交时；直线与函数没有交点但斜率相等、平行时；直线与函数有无穷多个交点，重合时。

八、解直线方程问题的方法

然后利用已知的条件进行求解，解直线方程问题时，可以根据题目的要求确定直线的方程。常见的解题方法包括：根据两点求解，根据与已知直线的关系求解等、根据点斜式求解，根据斜率截距式求解。

九、平行线和垂直线问题的解法

我们需要根据已知条件判断两条直线的关系，并求出符合条件的直线方程，平行线和垂直线问题中。常见的解题方法包括：利用已知直线求解平行和垂直关系，根据斜率判断平行和垂直关系。

十、应用题：直线与图形的问题

我们经常会遇到直线与图形的问题，在应用题中。进而解决问题，通过求解直线方程和图形的方程、我们可以确定直线与图形的关系。常见的应用题包括：直线与矩形，直线与三角形、直线与圆等。

十一、解方程组问题

直线方程经常与其他方程进行联立求解，在解方程组问题中。我们可以求解未知数的值，找到满足条件的解，通过联立直线方程和其他方程。常见的解题方法包括：几何法等，代入法，消元法。

十二、垂直距离的计算

可以根据已知的直线方程和点的坐标进行计算，垂直距离是指一个点到直线的垂直距离。我们可以求出点到直线的垂直距离、通过求解直线方程和垂直距离的方程。

十三、平行线的判定

我们需要比较它们的斜率，判定两条直线是否平行时。则它们是平行的，如果两条直线的斜率相等且不为无穷大。我们可以判定两条直线是否平行、通过斜率的比较。

十四、垂直线的判定

我们需要比较它们的斜率的乘积、判定两条直线是否垂直时。如果两条直线的斜率的乘积为-则它们是垂直的，1。我们可以判定两条直线是否垂直，通过斜率的乘积。

掌握直线方程是高二数学中的重要知识点。斜率截距式和点斜式，我们可以灵活运用直线方程解题、通过掌握直线的一般方程。以及解直线方程问题和应用题的方法、能够帮助我们更好地理解和应用直线方程，同时，了解直线与其他图形的关系。我们可以提高数学解题能力，轻松应对高二数学中的各种问题、通过学习直线方程。